Всичко за Форекс пазара и как се печели от него | dLambow

Какво е Форекс пазар и как се печели от него?

Форекс пазарът предлага на търговците огромна възможност да печелят от колебанията на валутните пазари. Валутният пазар е наистина огромен по обема на ежедневно сключваните сделки, но в същото време принципът му е доста прост, за разлика от други финансови пазари, което го прави много привлекателен и даже любим начин за заработване на доходи от къщи (през интернет).

Какво представлява Forex пазарът?

Пазарът за обмяна на валута (Forex или съкратено Fx) е глобален децентрализиран пазар, на който се търгуват валути. Няма обща, централизирана платформа за операции. Напротив, търговците и другите участници на пазара извършват транзакции по електронен път на принципа OTC (over-the-counter), т.е. извън борсата.

Защо се търгуват валутни двойки на форекс?

На обикновен пазар се търгуват различни стоки срещу пари. А щом на форекс стоките са пари (валути), това означава, че се търгуват пари (валути) срещу други пари (валути). Ако ще пътувате в Турция, отивате във валутното бюро и с левове си купувате турски лири. Ако ще отивате в Япония - купувате с левове японски лири.

Обърнете внимание, че всички покупко-продажби на валутния пазар се правят по валутни двойки. Защо е така? Защото не може да платите за лирите с череши. Трябва да платите с друга валута (левове, долари, евро...) с която разполагате. При това плащате според обменния курс, който е определен за съответната валутна двойка.

Операциите на валутния пазар включват едновременна покупка на една валута и продажба на друга. Това означава, че стойността на една парична единица може да бъде изразена чрез количеството на други парични единици. Следователно, когато купувате лира, вие в същото време продавате левове.

Какво е Форекс пазар?

От какво се печели на форекс?

Да се върнем на примера с турските лири. След като сте си купили турски лири, вие посещавате Турция и след една седмица се връщате. Турските лири повече не ви трябват и вие искате сега да ги продадете (върнете) и пак да получите левове. Но тази покупко-продажба на валутни двойки винаги става според курса в момента на сделката.

Повечето валути по света са "плаващи", т.е. курса им постоянно се променя.

Малко вероятно е на връщане от Турция да обмените лирите за левове по същия курс. Курсът или се е покачил или е спаднал. В зависимост от това, вие или ще спечелите или ще загубите от обратната продажба на лирите. Ето, това използват валутните търговци на форекс - постоянните промени на валутните курсове, като се стараят да сключват печеливши сделки и да избягват губещите.

Прогнозиране на валутните курсове на форекс

Когато търгувате на форекс, вие искате да печелите, а не да губите. За тази цел трябва да осъществявате печеливши операции. А за да са печеливши вашите операции с валути, трябва да умеете правилно да прогнозирате (познавате) промените във валутните курсове. За тази цел, обикновено, се използват три начина:

- Фундаментален анализ на пазара

Фундаменталният анализ е процес на анализиране на влиянието на политически, икономически и социални фактори върху относителната стойност на дадена валута. Чрез идентифициране на основните двигатели на присъщата стойност на дадена валута, форекс участниците могат след това да изработят информирани търговски решения.

- Технически анализ на форекс

Техническият анализ е изследване на историческото ценово поведение на валутните двойки, за да се идентифицират модели и да се определят вероятностите за бъдещи движения на пазара чрез използване на технически проучвания, индикатори и други инструменти за анализ.

- Графичен анализ на форекс пазара

Форекс диаграмата е графично представяне, показващо как цената на валутна двойка се променя с течение на времето. Цената се нанася върху вертикалната ос y, докато хоризонталната ос x показва времето. Често, пазарното поведение на валутните двойки е свързано с образуването на определени графични фигури или модели. Систематизирането и изучаването на тези модели помага в прогнозиране на валутните курсове.

- Четвърти начин да се печели без прогнозиране

За да разберете добре четвъртия начин (да печелите без да си играете с прогнози), първо трябва ясно да разберете двете понятия "диапазон" на промените и "ход" на валутната двойка. Ако гледате графиката на която и да е валутна двойка (независимо о времевия интервал), ще забележите, че курса осъществява едно постоянно зиг-загообразно движение, което изглежда произволно и хаотично.

В рамките на един ден валутната двойка EUR/USD има средно дневен диапазон на промените около 100-120 пипса. Но вътре в рамките на този дневен диапазон двойката не стои на едно и също място, а постоянно прави своите зиг-заги (нагоре-надолу). Ако в края на деня сумирате всички тези хаотични движения, може да установите, че двойката е "пропътувала" 20000-50000 пипса.

Тогава е логично, че ако откриете две две срещуположни позиции (една къса - продажба и една дълга - покупка) по текущия курс за момента, след известно време курсът ще тръгне в едната посока, при което едната позиция ще е на текуща печалба (примерно +20 пипса), а другата позиция ще е на текуща загуба (примерно -20 пипса).

В този момент закривате печелившата позиция и фиксирате +20 пипса печалба. След това изчаквате курса да се "наиграе" и да тръгне в обратната посока, докато и другата позиция излезе на +20 пипса и тогава я закривате, като фиксирате още +20 пипса печалба. Така без никакъв анализ и прогнози и при минимален риск (докато са отворени две срещуположни позиции, те взаимно се хеджират-застраховат), реализирате две печеливши сделки. : )

Начини за печелене от валутни двойки на форекс

Има два начина да спечелите на Форекс. Всяка валутна двойка се състои от базова валута (тя е на първо място) и котируема валута (тя е на второ място). Валутната двойка показва колко единици от котируемата валута (втората) ще са необходими за закупуване на единица от базовата валута (първата). Например, да вземем валутната двойка EUR/USD.

Вариант за печалба 1:

Ако смятате, че еврото ще се покачи спрямо долара, може да купите двойката EUR/USD. Купувайки или, с други думи, отваряйки дълга позиция на пазара, вие продавате котируемата валута и купувате базовата валута. Тоест купувате EUR/USD на по-ниска цена, за да го продадете на по-висока цена в бъдеще. Разликата ще бъде вашата печалба.

Вариант за печалба 2:

Ако смятате, че еврото ще спадне спрямо долара, продавате EUR/USD или отваряте къса позиция. В този случай за еврото купувате щатски долари.  Тоест продавате EUR/USD на по-висока цена, за да го купите на по-ниска цена в бъдеще. Разликата ще бъде вашата печалба.

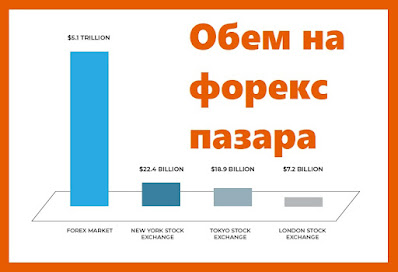Обем на форекс пазара

Търговската сесия на Форекс пазара

Пазарът за обмяна на валута никога не спи и котировките на него непрекъснато се променят. Това е единственият пазар, който работи 24 часа в денонощието, пет дни в седмицата. Търговията с валута в големи обеми се извършва на международния междубанков пазар в:

• - Цюрих,
• - Хонконг,
• - Ню Йорк,
• - Токио,
• - Франкфурт,
• - Лондон,
• - Сидни,
• - Париж

и други световни финансови центрове. Това означава, че междубанковият пазар е винаги отворен – когато в едната част на света приключи работният ден, в другото полукълбо, по това време, банките вече са отворили врати и търговията продължава.

Времева рамка за търговия

Липсата на времева рамка е много важно условие за търговците със свободен времеви график. Те не трябва да мислят за началния и крайния час на търговските сесии на междубанковия пазар, а да извършват транзакции по всяко удобно за тях време, тъй като за търговците на Forex пазара няма значение коя банка осигурява ликвидност за техните транзакции.

Ликвидност и обем на форекс

Ликвидността на Форекс също е много важна за инвеститорите, защото определя колко бързо ще се промени цената за всеки период от време. Огромната ликвидност на валутния пазар позволява многомилионни транзакции и тези транзакции почти не влияят върху динамиката на цените.
 
Въпреки това, не трябва да забравяме, че коефициентите на ликвидност могат да варират в зависимост от валутната двойка и времето на деня и по този начин да дават отражение върху търгуваните обеми, ако не на пазара като цяло, то поне на част от търгуваните валутни инструменти.

През деня ликвидността на Форекс пазара може да се промени в зависимост от банките в коя часова зона работят в момента (когато ликвидността спадне, спредовете се разширяват и скоростта на промените в цените се забавя). Например, по време на работата на японските банки най-ликвидните двойки ще бъдат с японската йена.

 

Обем на форекс пазара и значение за валутната търговия

Forex е съкратено от Foreign Exchange, което означава обмен на валута. Форекс пазарът е международния валутен пазар - най-големият и най-активен финансов пазар в света. Дневният му оборот надхвърля 5 трилиона долара. Това е повече от оборота на всички национални фондови пазари взети заедно.

Какво е обем на пазара (обем на форекс).

Валутният пазар FOREX, за разлика от други финансови пазари, като Нюйоркската фондова борса, няма конкретно местоположение. Той принадлежи към извънборсовите пазари, нарича се още "международен банков пазар". Международните банки са свързани помежду си в една мрежа и търговията се извършва в тази мрежа непрекъснато 24 часа в денонощието.

Всъщност това означава, че валутният пазар е разпределен повсеместно и може да се намира навсякъде по планетата. Международният междубанков FOREX пазар е най-популярният финансов пазар на планетата, където голям брой хора и организации участват в търговията. Това определя огромния му обем, който надвишава обемите на всички останали пазари.

Ежедневен обем на пазара.

Ако трябва да се направи оценка на форекс пазара, то тя е следната:  като ежедневен обем на конверсионните операции в света още през 1998 год. - той е бил 1.982 трилиона долара, а към днешна дата се оценява вече от 1 до 5 трилиона долара ежедневно (рекорд от 6.6 трилиона долара за 2019 г).

Разпределение на форекс пазара на дялове според търгуваните обеми

• - На Лондонския пазар се падат около 32% от оборота.
• - Часта на Американския пазар е около 18%.
• - На Германския - около 10%.

Операциите с участието на долара възлизат на около 70%. В днешно време, американския долар, като обем, участва в 90% от всички валутни сделки, които стават на forex пазара, като в това число са

• - евро — 37%,
• - йена — 20% и
• - фунт стерлинг — 17%.

По валутни двойки са така:

• - GBP/USD — 14%,
• - USD/JPY — 17% и
• - EUR/USD —28%

от целия обем валутни сделки на форекс.

Спекулации и обем на пазара

Едно от важните неща, които трябва да знаете за валутния пазар, е, че част от обема на търговията на FOREX са търговски и финансови транзакции, но по-голямата част от обема на търговията се формира от спекулативни транзакции с цел извличане на печалби от волатилността. Тоест повечето търговски операции на валутния пазар се извършват от търговци, които купуват и продават валути въз основа на краткосрочна динамика на цените.

Спекулантите заемат почти 80% от пазара.

Високият спекулативен компонент на валутния пазар създава огромна валутна ликвидност - тоест обема на покупките и продажбите, извършвани във всеки един момент. Следователно процесът на покупка и продажба на валута е лесен и достъпен за всеки от нас.
 

Технически индикатори за обем

Обемът на търговия на Форекс пазара се използва в някои технически индикатори, като се показва на търговските терминали на търговците. Показва се размера на промяната в стойността на търговските инструменти за определена единица време. Това по никакъв начин не отразява курса на валутата, участваща в транзакциите, и броя на самите сделки.
 
Но връзката между обемите на търговия и броя на транзакциите все още съществува, тъй като нивото на обема на търговия зависи от заявките за пазарни транзакции. За да разберат глобалните тенденции на Форекс пазара, експертите по търговия са разработили специални технически индикатори. Показанията на такива индикатори се използват преди всичко за анализиране на търговските стратегии на пазара, които се основават на фундаментални индикатори.
 
Сигналите на такива индикатори демонстрират общото настроение на Форекс участниците по отношение на съществуващите пазарни тенденции. Анализът на баланса на цените между абсолютните показатели на обемите на търговия ви позволява да реагирате по-чувствително на последиците, причинени от увеличаване или намаляване на цената на пазарните инструменти.
 

Търговия по обеми

Без съмнение, обемът на търговията на Форекс пазара има пряко влияние върху динамиката на цените на инструментите за търговия. Въз основа на показателите за обем се анализират цените на търговските инструменти. Много по-важни са индикаторите за промените в обема на търговия, тъй като анализите са именно динамиката на търговията и влияят върху съществуващите пазарни цени.

Търговецът може да вземе статистически индикатори за абсолютен обем за анализ и прогнозиране, но тук трябва да бъдете изключително внимателни, тъй като стойностите на абсолютния обем не са съществена информация.

Участници на Форекс пазара

Валутният пазар включва много и различни участници, които често се наричат "​​играчи" на Форекс пазара. Участниците търгуват с различни цели. Погрешно е да се мисли, че можете да извършвате търговски операции единствено с цел да печелите пари от промени в обменния курс. Всеки от участниците има своя собствена роля и като се допълват взаимно, те правят пазара по-устойчив.

Основните играчи на Форекс пазара са:

• - правителства и централни банки на страни
• - търговски банки и фирми
• - хедж фондовете
• - брокерски компании
• - инвеститори
• - индивидуални търговци
• - спекуланти

----------------

Откриване на търговски позиции на форекс | dLambow

Как се откриват търговски позиции при форекс търговия?

 

Механиката на форекс търговията

Механиката на всяка форекс транзакция предполага определена продължителност във времето. Началото на този интервал е отварянето (откриването) на търговска позиция по определена валутна двойка. Откриват се два вида търговски позиции:

• - или покупка на валутна двойка (откриване на дълга позиция - бай лонг/buy long) въз основа на предположението, нейният курс ще се покачва (възходящ тренд),

• - или продажба на валутна двойка (откриване на къса позиция - бай шорт/buy short) въз основа на предположението, че нейният курс ще спада (низходящ тренд).

Затварянето на позиция е обратна операция: търговецът продава това, което е било купено преди това, или обратно изкупува това, което е било продадено преди това на нова пазарна цена. Печалбата идва от курсовите разлики.

 

Какво е откриване на позиция на форекс?

Откриване на позиция при форекс търговия е ситуацията, при която валутния търговец е сключил сделка за покупка или за продажба на валутна двойка, но все още не е фиксирал финансов резултат по нея (т.е. позицията още не е закрита).

• - Ако търговец е закупил актив в очакване на поскъпването му, тогава той има отворена позиция за покупка (дълга позиция).

• - Ако търговец е продал валутна двойка в очакване на по-евтин актив, той има отворена позиция за продажба (къса позиция).

 

Автоматизъм при откриване на търговски позиции.

Откриването на търговски позиции на форекс трябва да доведете до автоматизъм, при това - до безгрешен автоматизъм, даже когато ситуацията на валутните пазари е най-напрегната, защото тогава трябва да се действа бързо и правилно. 

Откриване на търговски позиции на форекс

Ако не поработите върху техниката си на откриване на нови позиции, рискувате в напрегнати моменти да допуснете технически грешки, които да Ви костват доста сериозни загуби.

Опознаване на търговската платформа.

От момента, в който сте открили подходяща ситуация на валутния пазар, до откриването на позиция, трябва да изразходвате буквално секунди. Затова много упорито трябва да опознавате своята търговска платформа, до най-малките й тънкости.

Идентифициране на ситуация за търговия.

Веднага щом сте идентифицирали подходяща ситуация за търговия, според своите критерии, независимо как сте стигнали до нея, веднага откривайте позиция, ако искате да извлечете полза от нея, а не само да се занимавате с гледане (как другите печелят). Действайте веднага. Бездействието убива. Тук може да установите дали сте уверени в предишния етап - намирането на подходящи ситуации за откриване на позиции.

 

Упорити упражнения до автоматизъм.

Ако забележите съмнения или несигурност у себе си, върнете се на предишния етап и изгладете процедурите си там. Всичко това се постига с многократни и упорити упражнения, буквално по хиляди повторения. Така се добива автоматизъм, но и така набирате достатъчно материал за анализ и корекция на моделите си на вземане на решения, с оглед те да са по-успешни и печеливши.

Какво да правите на форекс?

Ако се колебаете какво да правите на форекс:

• - дали да откриете дълга позиция,
• - дали да откриете къса позиция

това със сигурност е губеща ситуация за Вас. Губещите губят, защото не са сигулни в собствената си подготвителна работа. А неувереността идва от липсата на опит на валутните пазари. Лечението е само едно, действайте на форекс упорито и постоянно тренирайте на демо сметка.

----------------

Какво са парите на форекс? | dLambow

 

Какво представляват парите на форекс?

Преди да разберем какво всъщност са "парите на форекс", нека с прости думи да си обясним съставките на това сложно понятие, а именно "какво са парите" сами по себе си и "какво е форекс" сам по себе си?

Какво са поначало парите?

Парите са:

• - средство за плащане на стоки и услуги,
• - средство за измерване на пазарни стойности и
• - средство за съхранение на търговска стойност. 

Парите са оценител за стойността на стоките и услугите, които се разменят в обществото чрез покупко-продажба. Чрез парите се осъществява стокообмен, плащания, измерване на стойността на нещо (в т.ч. и на хората), натрупване на капитал, инвестиране, спестяване... т.е. парите са средство за обмен. Парите обикновено са метални и книжни и имат различна номинална стойност, изписана върху тях.

Значение на парите

Парите обикновено са метални и книжни и имат различна номинална стойност, изписана върху тях. Чрез стойността си те служат за пазарно стоково разплащане. Но преди тях търговията се е провеждала чрез натурална размяна на стоки - бартер.

Бартерна размяна

Парите са заменили непосредствения, натурален обмен на стоки - бартера. При него се е налагало, ако имаш определена стока, да си намериш друг кандидат за размяна, който харесва твоята стока и има стока, която от своя страна ти трябва да харесаш и накрая да се договорите за количествата на размяната. 

 

Парично стокова размяна

След време се оказало, че парите са доста по-практични, удобни, универсални, издръжливи и сигурни като средство за съхраняване на стойност, отколкото натуралните стоки, които бързо се развалят и повреждат. Освен това, чрез тях обмяната на стоки става и значително по-евтина.

Какво са парите на форекс?

 

Парите имат пет основни функции

1. Мярка за стойност.

Парите ви позволяват да оцените стойността на стоките чрез определяне на цени.

2. Средство за размяна.

Парите играят ролята на посредник в процеса на размяна.

3. Начин на плащане.

Функция на парите, която позволява времето на плащане да не съвпада с момента на плащане, тоест когато стоките се продават на кредит.

4. Средства за натрупване и спестяване.

Способността на парите да участват в процеса на формиране, разпределение, преразпределение на националния доход, формиране на спестявания на населението.

5. Функцията на световните пари.

Тя се проявява във взаимоотношенията между икономическите субекти: държави, юридически и физически лица, разположени в различни държави.

Парите определят стойността на стоката

Количеството пари определят стойността (цената) на дадена стока. Но когато стоката е голяма и парите ставали цяла планина. Затова се появили леките, удобни книжни пари. Поради тези си качества, те лесно завоювали популярност. 

Да, но хората не знаят мяра и така започнали да се появяват пари в излишък. Как да ги съхраняват, какво да ги правят?

Постепено се появили „складовете“ за пари - банките. Тихи, уютни, безопасни. Появила се и идеята, съхранените пари, да се дават под наем - кредитирането. А след това и да се обменят срещу други валути и възникнал международния валутен пазар - форекс. 

Парите са уникални по своята простота. Те притежават и възможно най-високата ликвидност сред всички останали финансови средства. Т.е. те са носители на незабавна стойност. А на форекс те се превръщат и в стока, за която се плаща също в пари.

 

Парите са след бартера

Парите са заменили непосредствения, натурален обмен на стоки - бартера. При него се е налагало, ако имаш определена стока, да си намериш друг кандидат за размяна, който харесва твоята стока и има стока, която от своя страна ти трябва да харесаш и накрая да се договорите за количествата на размяната. Поради тази причина парите се оказали доста по-практични, удобни, универсални, издръжливи, сигурни.

Количеството пари са цената за стоката

Чрез парите обмяната на стоки става и значително по-евтина. Количеството пари определят стойността (цената) на дадена стока. Но когато стоката е голяма и парите ставали цяла планина. Затова се появили леките, удобни книжни пари. Поради тези си качества, те лесно завоювали популярност. 

Какво е Форекс с прости думи?

Форекс е валутния пазар, на който валутните търговците могат да обменят валути в реално време, от една страна - за да осъществяват основната си търговска дейност, а от друга - за да печелят от колебанията на обменния курс. 

Факт е, че котировките на валута една спрямо друга непрекъснато се променят, което позволява да се печели от промените им (от тяхната волатилност).

• - Ако купите (дълга позиция) правилната валута на ниска цена и след време я продадете, когато обменният курс се повиши, тогава можете да спечелите добри пари от разликата.

Или обратното

• - Ако продадете (къса позиция) правилната валута на висока цена и след време я купите, когато обменният курс се понижи, тогава можете да спечелите добри пари от разликата.

Основните валути, търгувани на Forex, са:

• - щатски долар,
• - евро,
• - лири стерлинги,
• - японски йени,
• - швейцарски франкове.

Въпреки това, можете също да търгувате с кръстосани курсове: това са валутните двойки, които не съдържат долара (USD). А ъсщо има и някои екзотични валути на страни от развиващите се пазари.

 

 А сега ...

Какво са парите на форекс?

На форекс парите са стоката, за която се плаща пак с ... пари. 

Парите са оценител за стойността на стоките и услугите, които се разменят в обществото чрез покупко-продажба. Чрез парите се осъществява стокообмен, плащания, измерване на стойността на нещо (в т.ч. и на хората), натрупване на капитал, инвестиране, спестяване... т.е. парите са средство за обмен.

Да, но хората не знаят мяра и така започнали да се появяват пари в излишък. Как да ги съхраняват, какво да ги правят? Така постепено се появили „складовете" за пари - банките. Тихи, уютни, безопасни. Така дошла идеята, съхранените пари, да се дават под наем (заем) - кредитирането. Парите са уникални по своята простота. 

Те притежават и възможно най-високата ликвидност сред всички останали финансови средства. Т.е. носители са на незабавна стойност. 

А на всичко отгоре, на форекс, те са и самата стока, за която се плаща пак ... с какво?? - с пари!

----------------

Защо умря Златния стандарт (Gold standard) | dLambow

Златен стандарт - златото в ролята на пари

Начало на златния стандарт.

През миналия век се сменят редица парични системи, колкото през цялата предшестваща стопанска история. Векът започва с биметализъм и златен стандарт, преминава през модифицираните форми на първоначалния златен монометализъм, създаване се хибридната (Бретън- Уудска) система и завършва с две полярни тенденции: свободно плаване между трите основни резервни валути и поява на нова валута (Еврото), която в принципите на организацията си връща към някои от фундаментите на златния стандарт.

Емисионните институти от началото на века представляват по правило частни банки. 

Впоследствие, редица от тях преминават през национализация, за да се превърнат след Втората световна война в съвременните централни банки. Основен проблем пред централното банкиране през цялото столетие е този за независимостта на паричната власт спрямо фискалната.

Златен стандарт (Gold standard)

Какво е златен стандарт?

Златният стандарт е парична система, при която валутата или книжните пари на дадена страна имат стойност, пряко свързана със стойността на златото. Със златния стандарт страните се съгласяват да конвертират хартиените пари във фиксирано количество злато. Страна, която използва златния стандарт, определя фиксирана цена за златото и купува и продава злато на тази цена.

По този начин, обезпечението на парите като разменно средство е известно като златен стандарт, сребърен стандарт или биметализъм, според същността на метала, който обезпечава парите. В световната платежна система, златния стандарт съществува до началото на 20- те години на миналия век или до началото на Първата световна война.

Сребърен стандарт

В световната система, освен златни, са се разменяли и сребърни пари в определено съотношение. Този двойнствен стандарт означава, че в обръщение са златни и сребърни монети, сечени свободно и без ограничение. Всички други платежни средства са поставени в зависимост спрямо златото и среброто. Крахът на биметализма се определя с развитието на търговията в международен мащаб.

Златен стандарт и атрибути на парите

Златният стандарт или златното обезпечение гарантира следните атрибути на парите:

- Мобилност на стойността

Парите могат да служат, за да бъде преместена стойността им от едно място на друго.

- Запазване на стойността

Парите запазват стойността си и я "транспортират" през времето.

- Размяна на стойността

Парите могат да се разменят за стоки и услуги. Някои от модерните валути са загубили този атрибут, доказателство за това е, че по време на прехода, редица стоки у нас /а и сега- жилища, автомобили/ се продават в щатски долари или евро, а не чрез лева.

Същност на златния стандарт

Същност на златния стандарт

До Първата световна война е съществувал т.н. Златен стандарт, т.е. златото е изпълнявало всички функции на парите, а книжните пари всъщност са се явявали негов представител и свободно са се обменяли за злато в съответсвие с указаното на тях златно съдържание. Тогава трудности с установяването на валутния курс не съществували.

Валутите са се базирали на валутния паритет.

Механизмът на действие на златните точки можел да действа само в условията на свободна покупка и продажба на злато по фиксирана цена и при отсъствие на ограничения по неговата доставка. Такава била ситуацията до Първата световна война. Златния век (1870 - 1914 г.) бил период на най-свободния капитализъм, познат в историята, и се е съпровождал с фиксиран курс на валутите.

Златен стандарт в България

Въпросът е решен по различен начин в отделните страни, като в края ХХ в. два от най- общоприетите принципи на икономическата теория са тези за необходимостта от максимална автономния на емисионната институция и за консервативна фискална политика. На този фон, българската парична система – подобно на всичко останало в икономиката – следва общия тренд с известно закъснение и видоизменение, понякога стигащо до неузнаваемост.

Крах на Златния стандарт (Защо умря златния стандарт?)

Възникналата в годините на Първата световна война инфлация направила невъзможен дотогавашния свободен обмен на валутите за злато и довела до крах на Златния стандарт. За кратко време той бил възроден през 1920 г. в модифициран, орязан вид. Но Световната икономическа криза от 1929 - 1933 г. довела и до неговия крах.

Нов валутен режим

Краят на златния стандарт предполага необходимостта от установяване на нов валутен режим. След края на този стандарт, същността на новата система има следното отношение към паричните стандарти:

• - Доларът е в качеството на международно платежно и резервно средство.

• - Формално английската лира също е с такъв статут, но още от самото начало на функционирането на Бретън - Уудс тя не е равностойна на долара.

• - Страните- членки на Бретън - Уудс могат да имат резерви в централните банки както в злато, така и в основни валути.

• - Споразумението задължава страните, поставили подписа си под него, да обявяват златното съдържание на националната си парична единица, да поддържат паритета. Валутата на една страна- членка на МВФ може да променя своята ценност само при условие, че настъпва фундаментално неравновесие в платежния й баланс.

• - Конвертируемост на валутите - възможност свободно да се придобива чужда валута чрез премахване на контрола върху размяната на операции по текущите сметки. Валутната конвертируемост за капиталовите операции се изключва като задължителна.

• МВФ е основната институция на новия валутен режим с кредитна, регулативна и техническо - консултативна функции. Заедно с него се изгражда и Международната банка за възстановяване и развитие.

Така, през 1931 г., Великобритания била принудена да отмени привързването на Фунта-стерлинг към златото. Започнал период на девалвации, периодично коригиране паритета на валутите, засилване на валутния контрол и вносни ограничения

Брентон - Уудска валутна система

Брентон - Уудската валутна система, създадена през 1944 г., била призвана да обедини твърдостта, присъща на Златния стандарт и гъвкавостта, отличаваща системата на колебаещите се курсове. Било фиксирано официално златно съдържание на националните валути на всички страни - участнички, и чрез него се определили взаимните паритети на валутите. Но не било вменено задължение да се обменят книжни пари за злато, поради което механизма на златните точки престанал да действа.

Но страните - участнички приели споразумение да не допускат отклонение на валутните курсове от паритета на повече от 1% + или -. Автоматичното изравняване на платежните баланси трябвало да става чрез промяна в доходите и цените като реакция на изменението на валутните резерви. Само в случаи на „фундаментален дисбаланс" е трябвало да се променят паритетите.

Ускоряване на инфлацията и девалвации.

Но през 60-те години започнали да се проявяват слабости на установената система. Забелязала се тенденция към ускоряване темповете на инфлация. Усилването на инфлацията и увеличаването на различията н нейните темпове, водели до периодични преразглеждания на паритетите.

Макар и Брентон - Уудс да се счита като пример за твърдо фиксирани курсове, за периода 1948 - 1967 г. националните си валутни курсове са променяли 109 държави, а средната обезценка на валутите била 48,2%. 48 държави провели повече от 1 девалвации на своите валути.

Златен долар.

В съответствие с Брентон - Уудското споразумение само САЩ гарантирали обмена на своята валута за злато по фиксиран курс, но да предявяват долари за обмен можели само централни банки на други държави. Освен това, такива стъпки се разглеждали като „недружеска" по отношение на САЩ акция и се осъществявали твърде рядко. По този начин френския президент Шарл де Гол успешно попълнил златния запас на Франция.

През 60-те години инфлацията ударила и САЩ.

Пазарната цена на златото започнала да надвишава фиксирана и САЩ не можели изкуствено да я поддържат. Така, на 15.08.1971 г., президента на САЩ Ричард Никсън, с един подпис ликвидирал съществуващата обвързаност между долара и златото и американската валута се лишила от своето обезпечение.

Режим на плаващи валути.

През декември 1971 г. било взето решение за девалвация на долара (първа в следвоенния период). Така от март 1973 г. режимът на плаващи валути става преобладаващ. Принципно изключение представлява режима на курсове в рамките на Европейската валутна система.

Ямайска валутна система.

Официално новия валутен ред, включително и прехода към плаващи курсове, бил фиксиран със споразумение, постигнато на конференцията в гр. Кингстоун, Ямайка. Обновеният Устав на МВФ не предполага повече обвързване на валутите към златото, което изключва установяването на на фиксирано съотношение между валутите на базата на златния паритет.

Така през 1976 г. Брентон - Уудската валутна система била заменена от Ямайската валутна система. Последната не изключва съглашенията за фиксирани курсове в модифициран вид, доколкото предвижда, че стран - членка на МВФ може по желание да избира като критерий за определяне паритет на своята валута или СДР, или една или друга валута, или валутна „кошница".

От това се възползваха европейските страни, които през 1979 г. създадоха Европейската валутна система, която в днешно време прерастна в единна валута - евро, макар че тя все още не е приета от всички европейски държави - Великобритания, Дания, Швеция, Норвегия, Швейцария, България, Румъния и др. Това е кратката история на Златния стандарт и валутния пазар, от златото като пари до плаващите курсове на валутите.

----------------

Парични единици | dLambow

Парични единици или знаци на държавите

Парични единици знаци (Currency signs)
1.	Dollar Symbol	$
2.	Euro Symbol	€
3.	Pound Sterling Symbol	£
4.	Yen Symbol	¥
5.	Franc Symbol	₣
6.	New Zealand dollar Symbol	$NZ
7.	Australian dollar Symbol	$A
8.	Canadian dollar Symbol	Can$, C$

Какво е парична единица?

Паричната единица на една страната е исторически или законодателно установения паричен знак, явяващ се основен елемент от паричната система на страната или единица за парично измерване. 

Физически носител на паричната единица са хартиените банкноти или копюри и металните монети, емитирани за осигуряване на паричното обращение в страната. Освен това, паричната единица има обръщение и в безналична форма за електронни банкови или картови разплащания между стопански субекти и физически лица.

Парични единици знаци (Currency signs)

Използване на парични единици в държавата

Парични единици, наричани и валути, в една държава се използват:

• - за изразяване на цените на стоките и услугите,
• - за установяване на номиналите на банкнотите на страната,
• - за извършване на парични сетълменти,
• - за извършване на счетоводни операции,
• - за определяне на стойността (курса) на чуждестранните валути.

От 70-те години на XX век, в резултат на демонетизацията на златото (загубата на неговите парични функции) и прехода на всички страни по света към използването на фиатни пари, металното съдържание на паричните единици, като правило, не се установява. 

Наименованието на паричната единица се определя от националната централна банка, но може да бъде фиксирана от конституцията на държавата или други закони.

 

Международни парични единици

През 30-те години на 20 век започват да се създават международни парични единици за международни разплащания и статистика. Например, Банката за международни разплащания използва златен франк, съдържащ 0,29 грама чисто злато.

• - През 1950-1958 г. в рамките на Европейския платежен съюз се появява европейска платежна единица (епунит от англ. EP-Unit - European Payment Unit), равна по златно съдържание на щатския долар.

• - През 1958-1978 г., тя е заменена от европейска счетоводна (парична) единица (англ. EUA - European Unit of Account), а

• - През 1979-1998 г. - от европейска валутна единица (ECU от англ. ECU - European Currency Мерна единица).

• - ECU беше заменено от еврото през 1999 г.

Международни валутни единици са и:

• - специалните права за тираж (СПТ от англ. SDR - Special Drawing Rights), от 1970 г., издавани от Международния валутен фонд, и

• - франкът CFA, използван в много страни от Централна и Западна Африка.

Някои страни отказват да използват собствените си парични единици в полза на националните валути на други страни. Най-популярни в това качество са такива парични единици, като щатския долари и еврото.

Какво е валута и за какво служат валутите (currency)?

Валута (от итал.: valuta - цена, стойност; от лат.: valeo - струвам; от англ.: currency) е всяка форма на парични единици (парични знаци, парични инструменти) или парични средства, използвани за:

• - законни разплащания,
• - погасяване на дългове,
• - измерване стойността на стоките

на територията на една държава, които са пуснати в обръщение от правителството и по-точно от Централната банка на държавата. Валута е паричната система на самата държава (златна, книжна). Валутните парични единици се използват също:

• - за международни разплащания,
• - за икономически обмен
• - за международни валутни отношения, свързани с парични разчети.

Паричните знаци от една валута могат да бъдат във вид на:

• - монети,
• - банкноти,
• - чекове,
• - полици,
• - парични преводи,
• - кредитни инструменти,
• - търговски документи

и други подобни инструменти, които се изплащат при предявяване или в определен срок.

Валута на плащане

Валутата на плащане е всяка валута, съгласувана между доставчика и купувача, с която става фактическото плащане на стоки или услуги по външно-търговска сделка или погасяването на международния кредит. Валутата на плащане се избора според:

• - валутния курс,
• - установените традиции,

и други подобни съображения. Валутата на плащане може да съвпада или да не съвпада (особено при клиринговата форма на разплащания) с валутата по сделката. При несъвпадане на валутата на плащане и валутата по сделката, трябва да се определи валутен курс за пресмятанията.

Валута на сделката

Валута на сделката е паричната единица, чрез която е отразена цената на стока по външнотърговски договор.  Валута на сделката се пределя с цел застраховане на риска от изменение валутния курс.

Основна валута в международната търговия.

В международната търговия, най-често използваните валути за плащания са американския долар, еврото, японската йена и някои други. Основна валута в международната търговия е американския долар. По-голямата част от международните разплащания се осъществяват в долари. Така се фиксират световните цени на много стоки.

Конвентируемост на валутите.

Свободно конвертируемата валута е тази, която свободно и неограничено се обменя за други валути. Съществуват още:

• - частично конвертируеми,
• - неконвертируеми валути.

Съществуват реални и условни парични единици.

Разпространение в международните отношения са получили „Специалните права за тираж" - изкуствено създадена международна разчетна парична единица. Съществуват още:

• - национални парични единици,
• - колективни парични единици (евро, арабски долар, андско песо),
• - международни валути (долар).

Парични единици на всички страни по света

1. Австралия — долар (австралийски) — AUD
2. Австрия — евро — EUR
3. Азербайджан — манат (азерб.) — AZM
   
4. Албания — лек — ALL
5. Алжир — динар (алг.) — DZD
6. Ангола — куанза — AON
7. Андора — евро — EUR
8. Антигуа и Барбуда — долар (Източни Кариби) — XCD
9. Антилски острови — гулден (антили) — ANG
10. Макао — патака — МОР
11. Аржентина — песо (арж.) — ARP
12. Армения — драм (арм) — ARD
13. Аруба — гулден (аруб.), флорин — AWG
14. Афганистан — афгани — AFA
15. Бахами — долар (Бахамски острови) — BSD
16. Бангладеш — така — BDT
17. Барбадос — долар (барб.) — BBD
18. Бахрейн — динар (бахр.) — BHD
19. Беларус — рубла (беларуска) — BLR
20. Белиз — долар (белиз) — BZD
21. Белгия — евро — EUR
22. Бенин — франк CFA — XOF
23. Бермудските острови — долар (берм.) — BMD
24. България — лев — BGL
25. Боливия — боливиано — BOВ
26. Ботсвана — пула — BWP
27. Бразилия — реал (браз.) — BRR
28. Бруней — долар (брун.) — BTN
29. Буркина Фасо — франк CFA — XOF
30. Бурунди — франк (бурунд.) — BIF
31. Бутан — ngultrum или рупия (бут.) — BTN
32. Вануату — вату — VUV
33. Ватикана — лира (ДДС) — VAL
34. Великобритания — Британски паунд — GBP
35. Унгария — форинт — HUF
36. Венецуела — боливар — VEB
37. Вирджински острови (САЩ) — американски долар — USD
38. Източна Самоа — американски долар — USD
39. Виетнам — донг — VND
40. Габон — франк CFA — XАF
41. Хаити — гурд — HTG
42. Гвиана — долар (гвайански) — GYD
43. Гамбия — даласи — GMD
44. Гана — седи — GHC
45. Гватемала — кетцал и щатски долар — GTQ, USD
46. Гвинея — франк (гвинейски) — GNF
47. Гвинея-Бисау — песо — GWP
48. Гибралтар — паунд (гибр.) — GIP
49. Хондурас — лемпира — HNL
50. Хонконг — долар (хонгконг) — HKD
51. Гренада — долар (Източни Кариби) — XCD
52. Гренландия — корона (датски) — DKK
53. Гърция — евро — EUR
54. Грузия — лари — GRL
55. Гуам — американски долар — USD
56. Дания — крона (датски) — DKK
57. Джибути — франк (джиб.) — DJF
58. Доминика (общност) — долар (Източни Кариби) — XCD
59. Доминиканска република — песо (Доминик) — DOP
60. Египет — паунд (Египет.) — EGP
61. Заир — заир — ZRN
62. Замбия — квача — ZMK
63. Западна Самоа — тала — WST
64. Зимбабве — долар (зимб.) — ZWD
65. Израел — шекел — ILS
66. Индия — рупия (инд.) — INR
67. Индонезия — рупия (индонезийски) — IDR
68. Йордания — динар (йордания) — JOD
69. Ирак — динар (Ирак.) — IQD
70. Иран — риал (Иран.) — IRR
71. Ирландия — евро — EUR
72. Исландия — корона (исландски) — ISK
73. Испания — евро — EUR
74. Италия — евро — EUR
75. Йемен (YAR) — риал (йеменски) — YЕR
76. Кабо Верде — ескудо — CVE
77. Казахстан — тенге — KZT
78. Кайманови острови — долар (острови Ким) — KYD
79. Камбоджа — риел — KHR
80. Камерун — франк CFA — XАF
81. Канада — долар (канадски) — CAD
82. Катар — риал (катарски) — QAR
83. Кения — шилинг (кен.) — KES
84. Кипър — паунд (кип.) — CYP
85. Кирибати — долар (австралийски) — AUD
86. Китай — юан — CNY
87. КНДР — вон — KPW
88. Колумбия — песо (колумбийско) — COP
89. Коморски острови — франк CFA — КМF
90. Конго — франк CFA — XАF
91. Южна Корея — вон — KRW
92. Коста Рика — колон — CRC
93. Кот-д’Ивуар — франк CFA — XOF
94. Куба — песо (куб.) — CUP
95. Кувейт — динар (Кувейт) — KWD
96. Острови Кук — долар (новозел.) — NZD
97. Киргизстан — сом — KGS
98. Лаос — кип — LAK
99. Латвия — лат — LVL
100. Лесото — лоти — LSL
101. Либерия — долар (либер.) — LRD
102. Ливан — паунд (ливански) — LBP
103. Либия — динар (либ.) — LYD
104. Литва — литас — LTL
     
105. Лихтенщайн — франк (Швейцария) — CHF
106. Люксембург — евро — EUR
107. Мавриций — рупия (Мавриций) — MUR
108. Мавритания — угия — MRO
109. Мадагаскар — франк (Мадагас) — MGF
110. Македония — денар — MKD
111. Малави — квача — MWK
112. Малайзия — рингит — MYR
113. Мали — франк CFA — XOF
114. Малдивите — руфия (малд.) — MVR
115. Малта — лира (малц) — MTL
116. Мароко — дирхам (мар.) — MAD
117. Мексико — песо (мекс) — MXP
118. Микронезия — американски долар — USD
119. Мозамбик — метикал — MZM
120. Молдова — леи (Молд.) — MOL
121. Монако — евро — EUR
122. Монголия — тугрик — MNT
123. Монсерат — долар (Източни Кариби) — XCD
124. Мианмар — кят — ММК
125. Намибия — южноафрикански ранд — ZAR
126. Науру — долар (австралийски) — AUD
127. Непал — рупия (Непал.) — NPR
128. Нигер — франк CFA — XOF
129. Нигерия — найра — NGN
130. Холандия — евро — EUR
131. Никарагуа — златна кордоба — NIO
132. остров Ниуе — долар (новозел.) — NZD
133. Нова Зеландия — долар (новозел.) — NZD
134. Нова Каледония — CFP франк — XРF
135. Норвегия — крона (норвежки) — NOK
136. остров Норфолк — долар (австралийски) — AUD
137. ОАЕ — дирхам — AED
138. Оман — риал (омански) — OMR
139. Пакистан — рупия (Пакистан) — PKR
140. Панама — балбоа, щатски долар — PAB, USD
141. Папуа-Нова Гвинея — кина — PGK
142. Парагвай — гварани — PYG
143. Перу — сол нов — PES
144. Полинезия френски — CFP франк — XРF
145. Полша — злоти — PLZ
146. Португалия — евро — EUR
147. Пуерто Рико — американски долар — USD
148. Русия — рубла (рос.) — RUR
149. Руанда — франк (руандийски) — RWF
150. Румъния — леи — ROL
151. Салвадор — колон, щатски долар — SVC, USD
152. Сан Марино — евро — EUR
153. Сао Томе и Принсипи — добра — STD
154. Саудитска Арабия — риал (саудитска) — SAR
155. Свазиленд — лилангени — SZL
156. Света Елена — Британски паунд — GBP
157. Сейшелски острови — рупия (сейш.) — SCR
158. Сенегал — CFP франк — XOF
159. Сейнт Винсент и Гренадини — долар (Източни Кариби) — XCD
160. Сейнт Китс и Невис — долар (Източни Кариби) — XCD
161. Сейнт Лусия — долар (Източни Кариби) — XCD
162. Сърбия — динар — YUD
163. Черна гора — динар — YUD
164. Сингапур — долар (синг.) — SGD
165. Сирия — паунд (сир.) — SYP
166. Словакия — крона (дума) — SLK
167. Словения — толар (словенски) — SКT
168. Соломонови острови — долар (Солом. острови) — SBD
169. Сомалия — шилинг (сомал) — SOS
170. Судан — динар (суд.) — SDD
171. Суринам — гулден (сурин.) — SRG
172. САЩ — американски долар — USD
173. Сиера Леоне — леоне — SLL
174. Таджикистан — рубла (тадж.) — TAR
175. Тайланд — бат — THB
176. Тайван — долар (тайв.) — TWD
177. Танзания — шилинг (танз.) — TZS
178. Того — франк CFA — XOF
179. Острови Токелау — долар (новозел.) — NZD
180. Тонга — паанга, долар (тонг.) — TOP
181. Тринидад и Тобаго — долар (Трин и Тоб.) — TTD
182. Тувалу — долар (австралийски) — AUD
183. Тунис — динар (тун.) — TND
184. Туркменистан — манат (турк.) — TUM
185. Турция — лира (тур.) — TRL
186. Уганда — шилинг (уганда) — UGS
187. Узбекистан — сума — UZS
188. Украйна — гривна — UKH
189. Острови Уолис и Футуна — CFP франк — XРF
190. Уругвай — песо (Уругвай) — UYP
191. Фиджи — долар (фиджи) — FJD
192. Филипини — песо (филлип.) — PHP
193. Финландия — евро — EUR
194. Фолклендски острови — паунд (фолк) — FKP
195. Франция — евро — EUR
196. Германия — евро — EUR
197. Хърватия — куна — HRK
198. КОЛА — франк CFA — XАF
199. Чад — франк CFA — XАF
200. Чехия — крона (чешки) — CZK
201. Чили — песо (чил.) — CLP
202. Швейцария — франк (Швейцария) — CHF
203. Швеция — крона (шведски) — SEK
204. Шри Ланка — рупия (Шри Лан.) — LKR
205. Еквадор — сукре, щатски долар — ECS, USD
206. Екваториална Гвинея — екуеле — -
207. Естония — крона (ест.) — EEK
208. Етиопия — бир — ETB
     
209. Южна Африка — ранд — ZAR
210. Ямайка — долар (ямайски) — JMD
211. Япония — йена — JPY

----------------

Форекс на автопилот | dLambow

Възможна ли е търговия на форекс чрез автопилот?

Автопилот за търговия на форекс

Форекс на автопилот е златната мечта на всеки валутен търговец.

Не е нужно да седите пред монитора с часове, да анализирате пазара и да търсите входни точки. Не се налага да настройвайте алармата за 3 часа сутринта, защото това изисква избраната от вас стратегията за търговия. И като цяло, просто правете печалба от търговия на автопилот. Но как да направите това? Кой ще търгува, ако търговецът не го направи сам? Нека го разгледаме по-внимателно.

- Автоматизиране на валутна търговия.

Има търговци, които си въобразяват, че процеса на валутна търговия може да се автоматизира. Те се стремят да си разработят собствена такава или да закупят готова от "специалисти". Много хора си хвърлят парите за "покупка на професионализъм", без да разбират, че в случая става дума за мързел, алчност и елементарна неграмотност.

- Автоматична търговия на форекс.

За сега системите за автоматична търговия на форекс са обогатили най-вече своите създатели. Сложната човешка дейност не подлежи на автоматизация. Компютърните системи не са в състояние да заменят хирурга при операция или Христо Стоичков пред противниковата врата. Компютрите могат само да подпомагат човека, но не и да го заместят. Използването на автопилот в самолетите не означава, че някой ще пусне самолет с 300 пътници на борда без отлично подготвени живи пилоти. 

Форекс на автопилот

Варианти за валутен автопилот

Все пак, има няколко начина за създаване на валутна търговия на автопилот:

• ● използване на търговски роботи (съветници);
• ● ползване на доверително управление на капитала;
• ● привличане на търговци чрез партньорска програма.

Всеки вариант е съвсем реален и изисква специфичен подход. Но тези, които са инвестирали времето и усилията си за прилагане на един или повече от тези методи, всъщност са създали пасивен доход за себе си – тоест правят печалба с Forex с малко или никакви усилия и време или други разходи. Това е интересно за умните хора, които искат да опростят живота си и да правят печалби с форекс на автопилот.

Търговски роботи (съветници) за автоматична търговия

Търговските експерти са програми, които могат да търгуват по даден алгоритъм без участието на търговеца. Идеалният робот трябва да прави печалба в дългосрочен план или да търгува агресивно, така че печалбите да покриват дългосрочните загуби за кратки периоди от време.

Всички останали случаи на използване на съветници не си струват прекараното време. Първото нещо, което трябва да направите със съветника, е да го тествате. Обърнете специално внимание не само на индикатора за рентабилност, но и на продължителността на печелившата търговия.

Не е задължително добрият съветник да струва скъпо, той може да бъде даже безплатен. Но предпоставка за пълното развитие на робота е разбирането на принципите за неговата търговия. Ако не знаете с каква схема (стратегия) търгува роботът, той ще остане черна кутия, което означава, че може да загуби вашия депозит по всяко време. 

Доверително управление

Доверителното управление е много популярен метод, който продължава да набира скорост сред търговци и инвеститори. Всъщност търговецът става инвеститор, но може напълно или частично да проследява търговията на управляващия търговец, като по този начин променя нещо в неговата търговия. Има и услуги за пълно копиране на сигнали от терминалите на успешни търговци.

Всичко, от което се нуждае един търговец-инвеститор, за да реализира печалба, е да анализира търговската статистика на управляващите търговци и да разпредели средствата за тях. Не е желателно да се гонят свръхпечеливши индикатори, а да се фокусирате върху стабилна дългосрочна търговия.

Привличане на търговци чрез партньорска програма

Не е тайна, че търговските терминали плащат част от спреда от сделките, закрити от търговеца, на своите партньори, които са поканили търговеца да се регистрира в съответната платформа. Тук, решаващото е да работите с надеждни платформи, които сте проучили внимателно.

Привличайки търговци за търговия, с течение на времето можете да получавате стотици и хиляди долари на месец пасивен доход. Но първо трябва да свършите добра работа. Предложете на търговеца печеливша стратегия, достъп до безплатни сигнали или тайна техника за търговия като бонус за регистрация и той с удоволствие ще стане ваш реферал.

Непредвидени ситуации на форекс.

В сложната дейност винаги има непредвидени ситуации, с които машината не може да се справи. Така е и на Форекс. Едно непредвидено обстоятелство и дотук с Вашата сметка и мечти за търговия - релакс. Иначе е привлекателно да се събудиш сутринта към 9 часа, след сладък сън, да си сложиш кафето, да врътниш копчето на автопилота за валутна търговия и докато си пиеш кафето пред телевизора, да спечелиш няколко хиляди за джобни пари през деня. Мечтиии..., както се казва в една реклама.

----------------

Теория на хаоса | dLambow

Теория на хаоса (ТХ) във валутната търговия на форекс

Какво е хаос?

Философско-митично значение на хаоса

Хаос (от старогръцки: χάος от χαίνω - разкривам се, развръщам се) е категория на космогонията и космологията:

• - Първичното състояние на Вселената, безформена комбинация от материя и пространство (за разлика от реда). Първичното безформено и безпорядъчно състояние на света, неорганизирана стихия, изпълнена с мъгла и мрак.

• - Идеите за епохата на хаоса възникват в резултат на развитието и конкретизирането на представите за митичното време, особен начален сакрален период, предшестващ емпиричното (историческото) „профанското” време.

• - Едно от въплъщенията на хаоса или самия хаос, често е световният океан, първобитните води. В много древни космогонични митове океанът и хаосът са еквивалентни и неразделни един от друг.

• - Концепция, използвана в планетарната геология за описване на области на повърхността на небесните тела, които имат хаотичен релеф.

Теория на хаоса

Обикновено значение на понятието за хаос

В обикновения смисъл хаосът се разбира като безредие, безпорядък, объркване, смесване, отсъствие на ред. Хаосът е състояние, при което е много трудно или дори невъзможно да се предвиди развитието на определена система в бъдеще. Грубо казано, това е объркване, липса на яснота и хармония в организацията на системата. 

Все пак трябва да се отбележи, че хаосът не трябва да се счита само за вредно явление, което може само да обърква. Хаосът може и трябва да се изучава, освен това може да се приложи в практиката. Например концепцията за хаоса е много важна за синергетиката, тоест координираното взаимодействие на елементите при формирането на система. Освен това, в известен смисъл, дейността на хората, като елементи на обществото, често е хаотична, спонтанна.

Изучаването на хаоса може да бъде полезно за социологията при изучаването на обществото и дейността на хората като негови елементи. Икономисти, математици, физици и др. признават, че това е само едно от състоянията на системата, характеризиращо се с определени закони за управление.

Концепция за хаоса

Концепцията произлиза от името в древногръцката митология на първоначалното състояние на света, един вид „отворена бездна” (а не безпорядъчно състояние), от която произлизат първите божества. Едва в ранните християнски времена, понятието получава значението на безпорядък.

Хаос в математиката

В математиката хаосът е апериодичното детерминирано поведение на динамична система, която е изключително чувствителна към началните условия. Безкрайно малко смущение на граничните условия за хаотична динамична система води до крайна промяна в траекторията във фазовото пространство. Изучава се с математически средства на теорията на хаоса.

Хаос и ентропия

За количествено измерване на случайността (разстройството) на дадена система във физиката и математиката (теория на информацията, математическа статистика) често се използва понятието ентропия, което едновременно характеризира информационния капацитет на системата.

Какво е Теория на хаоса?

Теорията на хаоса е математически апарат, който описва поведението на някои нелинейни динамични системи, които са подложени, при определени условия, на явление, известно като хаос (динамичен хаос, детерминиран хаос). Поведението на такава система изглежда случайно, дори ако моделът, описващ системата, е детерминистичен. За да се подчертае особената природа на явлението, изучавано в рамките на тази теория, е обичайно да се използва името "динамична теория на хаоса".

Примери за хаотични системи са:

• - атмосферата,
• - турбулентните потоци,
• - някои видове сърдечни аритмии,
• - биологичните популации,
• - обществото като комуникационна система и неговите подсистеми:
• = икономически,
• = политически,
• = психологически (културно-исторически и междукултурни) и
• = други социални системи.

Тяхното изследване, наред с аналитичното изследване на наличните рекурентни отношения, обикновено е придружено от математическо моделиране. Теорията на хаоса е област на изследване, която свързва математиката и физиката.

Основна информация за Теория на хаоса

Теорията на хаоса казва, че сложните системи са изключително зависими от първоначалните условия, при което даже малките промени в околната среда, могат да доведат до непредвидими последици за системата като цяло.

Математическите системи с хаотично поведение са детерминистични, тоест те се подчиняват на някакъв строг закон и в известен смисъл са подредени. Тази употреба на думата "хаос" се различава от обичайното й значение на безпорядък, липса на ред. Отделна област на физиката - теорията на квантовия хаос - изучава недетерминирани системи, които се подчиняват на законите на квантовата механика.

Пионери на теорията за хаоса са френският физик и философ Анри Поанкаре (той доказа теоремата за повтаряемостта), руските математици А. Н. Колмогоров и В. И. Арнолд и немският математик Ю. Мозер. Теорията въвежда концепцията за атрактори (включително странни атрактори, като привличащи Кантор структури), стабилни орбити на система (т.нар. KAM-торове).

Теория на хаоса на форекс

Теория на хаоса е един от най-модерните подходи за изследване на валутния пазар и търговия на форекс. Но все още не съществува точно математическо определение за хаос. В момента той се определя като крайна неопределеност на постоянно нелинейно и нередовно сложно движение, възникващо в динамична система.

Хаосът не е случаен, независимо, че е непредсказуем.

Той е динамично определен. На пръв поглед непредсказуемостта граничи със случайността, а случайни явления не могат да се предсказват. Ако се отнасяме към пазара като към случайни блуждения, то това е самият случай. Но в хаоса има определени закономерности. Хаотичното движение на цените не е случайно, а друг вид подреждане. Непредсказуемостта на хаоса се обяснява  основно от съществената зависимост от началните условия. Тя показва, че даже най-малки грешки при измерване на параметрите, могат да доведат до съществени и абсолютно неверни предсказания.

Теория на хаоса на форекс пазара

 

 

 

 

 

Грешки и неточности в хаотичните системи

Тези грешки могат да възникнат от елементарно незнание на всички начални условия. Нещо непременно се изплъзва от вниманието. Така в задачата се залага вътрешна грешка. Допълнителни неточности могат да се внесат и от неточното измерване на най-незначителни външни или вътрешни фактори за въздействие върху пазара.

Пример за хаотично движение е билярдната топка.

Крайния резултат от удара зависи от множество фактори. И най-малката неточност в един от тях води до непредсказуеми резултати. Даже всичко да е съвсем точно, опитайте се да предскажите пътя на топката само след 3 - 4 удара.

Главен извод за хаоса

Един от главните изводи в ТХ е, че не може да се предскаже бъдещето, тъй като винаги ще възникват грешки в измерванията, породени, в т.ч. и от незнание на всички фактори. При това малки изменения или грешки могат да предизвикват големи промени или откронения в системата.

Експоненциална грешка.

Друго основно свойство на хаоса е експоненциалното натрупване на грешки. Което означава, че нарастването на грешките ще става бързо, далеч зад допустимата предсказуемост. Следователно достоверността на прогнозите с времето зночително спада. Този извод е съществена пречка за приложимостта на Фундаменталния анализ, който оперира именно с дългосрочни критерии.

Хаосът е друга форма на порядък.

Движенито от порядък към хаос и обратното е същност на вселената. Даже в човешкия мозък съществуват подредени и хаотични начала. Порядъка е в лявото полукълбо (съзнателните действия), а хаоса в дясното (интуицията). ТХ изучава порядъка в хаотичната система и помага да се построи модел на такава система, без да си поставя за задача да предсказва точно поведението на системата.

С какви инструменти разполага ТХ?

Това са преди всичко атракторите и фракталите.

Атрактора  (attract - привличам)

е геометрична структура, характеризираща поведението във фазовото пространство за продължителен период от време.

Фазовото пространство

е абстрактно пространство, чийто координати се явяват степените на свобода на системата. Например, в движенията на махалото има две степени на свобода. Това движение е напълно определено от началната скорост на махалото и от негото положение. Ако не съществува съпротивление, то фазовото пространство на махалото ще е затворена крива. Но поради въздействието на триенето, то реално фазавата пространство е слирала.

Атрактора е това, към което се стреми системата, това което я привлича.

 

Най-простия атрактор е точката.

Такъв атрактор е характерен за махалото при наличие на триене. Независимо от началната скорост и положение, махалото винаги си стреми към покой в една точка.

Друг вид атрактор е пределния цикъл,

който има вид на затворена крива. Такъв пример е махалото, на което не му влияе силата на триене. Такъв пример е и биенето на сърцето. Честотата на биене може да намалява и да се увеличава, но тя винаги се стреми към своя атрактор, своята затворена крива.

Основни видове атрактори.

• Прости предсказуеми атрактори атрактори.
• Хаотични атрактори.

Независимо от сложността на поведение на хаотичните атрактори, познаването на фазовото пространство позволява да поведението на системата да се представи в геометрична форма и съответно да се предсказва. И макар, че е невъзможно да се определи в конкретен момент от време точно къде се намира системата, то областа на пребиваване и стремежът към атрактора са предсказуеми.

Атрактор на Лоренц

Той има три степени на свобода - три обикновени диференциални уравнения, три константи и три начални условия. И макар, че е прост, то тази система се държи хаотично. Моделирана на компютър, тази система показва своя хаотичен характер - даже най-малките отклонения в началните условия, в процеса на еволюция водят до големи, експоненциални грешки. 

Но този атрактор има крайни размери, т.е. раздалечаването между двете системи не може да е безкрайно и все някога се преминава към събиране. По този начи, постоянното свиване и разпускане на хаотичния атрактор, систематично отстранява първоначалната информация и я заменя с ново.

При сближаване на траекториите се получава ефекта на късогледството - нараства неопределеността на едромащабната информация. При раздалечаване на траекториите обратно, се появява ефект на дългогледство - нараства неопределеността на дребномащабната информация. Следователно, с времето неопределеността стремително нараства, което ни лишава от възможността да правим точни прогнози.

Основно свойство на хаотичните атрактори.

В хаотичните системи не е възможно да се установи връзката причина - следствие. Причино - следствена връзка между миналото и бъдещето в хаоса няма. Скоростта на сближаване и раздалечаване е мярка за хаоса, т.е. числов израз колко е хаотична системата. 

Друга статистическа мера за хаоса е размерността на атрактора. Така, основно свойство на хаотичните атрактори е сближаването и раздалечаването на траекториите на различни системи, които по случаен начин, постепено и безкрайно се смесват.

Фракталът е противоположност на хаоса.

Той е статично явление, а хаоса е динамично явление. Фракталът е геометрична фигура, определена част от която се повтаря отново и отново, откъдето и свойството на фрактала - самоподобие. Друго свойство е дробността - математическо отражение степента на неправилност на фрактала. Всичко, което е случайно и неправилно, може да бъде фрактал. Облак, дърво, биенето на сърцето, популациите и миграциите на животните, езика на пламъка. Всеки фрактал се получава чрез поредица итерации - повторения.

Хаотичния атрактор е фрактал.

В техническия анализ на валутния пазар типичен фрактал са вълните на Елиот с принципа на самоподобието. Допълнителната идея, заложена във фракталите са нецелите измерения. Обикновено говорим да едно-, дву-, три-мерно измерение. Но могат да съществуват и нецели измерения . Това са т.н. фрактални измерения. В природата едва ли има идеални форми - кълбо, куб... Следователно, за тяхното описване не могат да служат целите пространствени измерения. За измерването на неправилните фрактални фигури се въвежда понятието фраткално (нецяло) измерение.

Има прости и сложни фрактали.

• Първите не изискват формули или уравнения. Взема се лист хартия, нанасят се няколко повторения на дадена фигура и готово. 

• За сложните фрактали е присъща безкрайна сложност, макар че тя е генерирана от проста формула. 

Класически пример за това е множеството на Манделброт, получавано по формулата:

Zn + 1 ≠ Zna + Cq

където

• Z и C - са комплексни числа
• а е положително число

Към хаос системите могат да преминават по различни начини.

Един от тях е бифуркацията (bifurcus - раздвоение). Това е процес на КАЧЕСТВЕН преход от състояние на равновесие към хаос, чрез последователно, много малко изменение на периодичните точки. Това става с т.н. катастрофични скокове. Момента на скока става в точката на бифуркация.

Хаосът може да възникне чрез бифуркация.

Анализира се уравнението

Хп + 1 = С(Хп)2,

където

• С - външен параметър.

Следователно, при някои ограничения,  с всички подобни уравнения става преход от равновесие към хаос. Да вземем пример от биологията:

Дадена популация живее изолирано и наброява Хп. След 1 година се появява потомство с численост Хп+1. Ръстът на популацията се описва от първия член от първия член на дясната част на уравнението (СХп), където коефициента С определя скороста на растеж и е определящ параметър. Измирането на животните поради пренаселеност и недостиг на храна се определя от втория, нелинеен член (С(ХП)2).

• - при С < 1 популацията с ръст п измира
• - в областта 1 < С < 3 числеността на популацията остава постоянна ХО = 1 - 1/С
• - при С = 3 точкта на бифуркация става отблъскваща фиксирана точка. От този момент функцията вече никога се събира към една точка.
• - в диапазона 3 < С < 3.57 започват бифуркации и разклонение на всяка крива на две. Отначало популацията рязко нараства. На следващата година се получава преселеност и след година числеността отново намалява.
• - при С > 3.57 става припокриване на областите с различни решения и поведението на системата става хаотично.

Следователно, заключителното състояние на еволюиращите физически системи е състоянието на динамичен хаос. Ето прехода от хаос през бифуркация.

Точка на бифуркация

Динамичните променливи Хп приемат стойности, които силно зависят от началните условия. Състоянието на системата в момента на бифуркация е крайно неустойчиво и безкрайно малко въздействие може да доведе към следващ път на движение - което си е хаос. Има универсални закономерности на преход към динамичен хаос при удвояване на периода, експериментално потвърдени за различни видове системи. Това се визуализира чрез т.н. Дърво на Фейгенбаум.

Какво е бифуркацията, казано на прост език?

Както разбрахме, бифуркацията възниква при преход на системата от стабилност и равновесие към хаос. Такива примери са дима, водата, и много други обичайни природни явления. Повдигащия се нагоре дим, отначало изглежда като стълб. Но след определено време, той претърпява изменения, които отначало изглеждат правилни, но след това се превръщав в хаотични и непредсказуеми. Фактически, първия преход от стабилност към някаква подреденост става в първата точка на бифуркация.. След това броя на бифуркациите се увеличава, достигайки огромни стойности и с всяка бифуркация движенията на дима се приближават до хаоса.

Приложения на бифуркацията.

С помощта на бифуркацията може да се предсказва характера на движението, възникващо при прехода на системата в качествено друго състояние, а също и областта на съществуване на системата и да се оцени нейната устойчивост. Самата теория на хаоса е трудно съвместима със съществуващите класически науки.

Хаосът е непредсказуем.

И когато се изучава хаотична система, може да се прогнозира само модела за нейното поведение. Затова с помоща на хаоса не трябва да се строят точни прогнози. За сега не съществува математически точен апарат за приложение теорията на хаоса при изследване на пазарните цени. Но това е перспективно съвременно направление на математиката от гледна точка на приложните изследвания на финансовите пазари.

 

Теория на хаоса при валутната търговия на форекс пазара

На пръв поглед, това което се случва на форекс пазара е хаос - възходящ тренд, нисходящ тренд, корекции, странично движение, волатилност, гапове и всичкото това съпроводено с много фонов шум. Това е така, когато сме застанали вътре в пазара и наблюдаваме форекс от близо. Но ако приложим Теория на хаоса, първото, което можем да направим, е да намалим с една стъпка хаоса, като "поставим" форекс пазара в една "колба". Течността в колбата се движи хаотично, но целия този хаос става вътре в колбата, а не отвън.

 

Как да поставим Форекс в колба?

• 1. От всичките, няколко десетки валутни двойки, ние вземаме само една - например, евро/долар. Това веднага намалява хаоса 10, 20 или 50 пъти.

• 2. Намираме потиковите исторически котировки за избраната валутна двойка (евро/долар) за поне 10, 15 или 30 години назад. Колкото по-пълна информация съберем, толкова по-добре.

• 3. Вкарваме събраните данни в таблица: време / котировки и получаваме една дълга графика. Първото, което ще забележим в тази графика е, че котировките имат минимум и максимум. Прекарваме по една линия през максималната и през минималната котировка (правим т.н. хоризонтален канал) и ... ето я "колбата" - избраната валутна двойка се движи "хаотично", но в рамките на този канал (вътре в него, а не извън него).

• 4. Започваме да правим анализ за поведението на курса по всички възможни начини, които могат да ни хрумнат (японски свещи, фрактали, волатилност, трендове, корекции и т.н. и т.н.). Целта е да намерим закономерности в поведението на валутната двойка.

 

Ето ви идеи:

• - Разделете графиката на седмични периоди и подредете седмичните периоди един под друг. Така може да забележите закономерности, които са свързани с дните от седмицата - какво става обикновено в понеделниците, във вторниците и т.н.

• - Прекарайте през цялата графика хоризонтални линии през 10 (20, 30...) пипса и изследвайте колко единични, двойни, тройни и т.н. пресичания на тези линии има в една посока. Когато кърса пресече линия нагоре, а след това се върне и пресече линия отдолу - това е странично движение. Когато курса пресече последователно 2, 3 или повече линии нагоре - това е възходящ тренд, а когато след това се върне 1-2 линии надолу - това е корекция и т.н.
• - продължете и с други изследвания ...

 

Собствена търговска система

Колкото повече научавате за поведението на избраната валутна двойка, толкова повече хаоса ще намалява и толкова повече идеи ще ви идват за начините, с които да печелите от форекс. И това е началото на изграждане на собствена търговска система.

Не е възможно да вземете чужда търговска система и да печелите наготово с нейна помощ, защото не я познавате. Единствения начин да печелите редовно и предвидимо от форекс е като създадете собствена търговска система и постоянно я подобрявате. На този сайт ще намерите много идеи за подобрение и развитие...

----------------